H. Kerkow ¹⁾ und B. Lukasch ²⁾, 1995:

Bemerkungen zum dynamischen Auftrieb

 Einführung

Die Entstehung des Auftriebs an der Tragfläche wird unterschiedlich erklärt und veranschaulicht. Otto Lilienthal hatte die Vorstellung, dass jedes Volumenelement Luft in der Nähe der gekrümmten Oberfläche eines Tragflügels eine entsprechende Bahnkurve beschreibt, also aus seiner geradlinigen Flugbahn kontinuierlich abgelenkt wird. Diese Radialbeschleunigung, verursacht durch den Tragflügel, hat als Reaktion den dynamischen Auftrieb zur Folge.

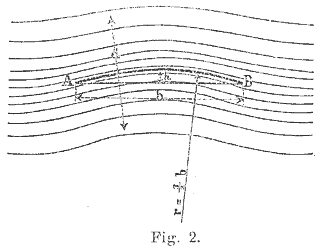
Abbildung aus: Otto Lilienthal: "Die Profile der Segelflächen und ihre Wirkung";
Zeitschrift für Luftschiffahrt, 1895, Heft 2/3, S. 42-57

In Lehrbüchern weit verbreitet ist die Erklärung durch unterschiedliche Bahngeschwindigkeiten der Luftströmungen ober- und unterhalb der Tragfläche. Sie sind auch durch eine der Luftbewegung überlagerte Zirkulation der Luft um den Flügel beschreibbar, verursacht durch einen Anfahrwirbel, dem aus Gründen der Drehimpulserhaltung die Zirkulation um den Tragflügel zur Kompensation überlagert werden muss. Ergebnis ist eine erhöhte Geschwindigkeit der Luft oberhalb der Tragfläche und eine niedrigere unterhalb (z. B. R. W. Pohl: "Einführung in die Physik" Bd.1, 1955 und F. Kuypers: "Physik für Ingenieure und Naturwissenschaftler" Bd.1, 2002).

Unterschiede in den Geschwindigkeiten werden auch durch eine Unsymmetrie in der Aufteilung des Luftstromes erklärt, wonach ein größerer Anteil der Strömung oberhalb der Tragfläche entlang gleitet und sich unter Annahme einer konstanten Dichte (Inkompressibilität) der Luft demzufolge dort mit einer höheren Geschwindigkeit bewegen muss. Die Geometrie des Tragflügels (analog dem Prinzip der Venturi-Düse) kann derartige Verteilungen hervorrufen. Die unterschiedlichen kinetischen Energien der Luftteilchen verursachen unterschiedliche statische Druckverteilungen an der Tragfläche (Bernoullische Gleichung) und bewirken so den dynamischen Auftrieb.

Aus den beiden letzten Modellvorstellungen folgt, dass erstens der Auftrieb leistungslos erzeugt wird, weil Bewegung und Kraft senkrecht aufeinander stehen, und es zweitens hinter dem Tragflügel zu einem Druckausgleich zwischen den oberen und unteren Luftschichten kommt, so dass es zu keiner nennenswerten Veränderung der Strömung relativ zum Tragflügel kommt. Doch an der Zweckmäßigkeit dieser Vorstellungen sind Zweifel angebracht. Flieger und Physiker sehen die seit einem Jahrhundert angebotene Veranschaulichung des dynamischen Auftriebs über die Bernoulli-Gleichung als unglücklich an.

Der Schwerpunkt der hier vorgestellten Untersuchungen soll auf die Frage gerichtet werden, ob die grundlegende Annahme einer konstanten Dichte der Luft bei der Strömung um die Tragfläche gerechtfertigt ist.

Beschreibung der Experimente

Hält man einen glühenden Draht in eine Luftströmung, so sinkt seine Temperatur, weil durch Konvektion Wärme an den Luftstrom abgegeben wird. Die vom Draht an die Luft abgegebene Leistung berechnet sich nach der Formel P_s = κ G v ρ (T_s –T_u), wobei κ die Wärmeübergangszahl, G ein Geometriefaktor (z.B. die aktive Oberfläche des Drahtes), v*ρ das Produkt aus Geschwindigkeit und Dichte der Luft, sowie T_s und T_u die Temperaturen des Drahtes bzw. der anströmenden Luft sind. Hält man die zugeführte elektrische Leistung mit der der Draht zum Glühen gebracht wird konstant, so stellt sich im Luftstrom eine Drahttemperatur ein, bei der die zugeführte Leistung gleich der abgegebenen sein muss.

Die Temperatur des Drahtes hängt dann nur von der Geschwindigkeit und der Dichte der Luft ab, wenn die übrigen Bedingungen der Wärmeabfuhr gleich bleiben. Über eine Temperaturmessung des Drahtes bekommt man also ein Maß für Geschwindigkeit und Dichte des Luftstromes. Da Temperaturänderungen im Prozentbereich zu erwarten sind (gewöhnlich der Bereich der Fehlergrenzen der Messung), sind Temperaturmessungen mit hoher Genauigkeit erforderlich. Deshalb wurde als Thermometer ein Thermistor benutzt, der mit einer Heizwicklung umgeben wurde, die durch eine Vergußmasse in einen innigen Wärmekontakt zum Thermistor gebracht war. Die Sonde hatte einen Durchmesser von 2,5 mm und war 7 mm lang.

Bei den Messungen lag die Zylinderachse der Sonde immer senkrecht zum Luftstrom, aber parallel zur Oberfläche der Tragfläche. Da der Thermistor einen negativen Temperaturkoeffizienten besaß, stieg sein Widerstandswert, wenn die Kühlung intensiv, also das Produkt aus Dichte und Geschwindigkeit groß war. Für eine qualitative Betrachtung war es deshalb ausreichend, die Verteilung der Widerstandswerte der Sonde zu messen, obwohl durch eine Eichung auch quantitative Aussagen möglich wären. Die Sonde war an einem langen Arm befestigt um die Beeinflussung der Strömung gering zu halten.

Es wurden Modelltragflügel mit einer Breite und Länge von 200 mm und einer Dicke von weniger als 20 mm verwendet. Ein Luftstrom von etwa 10 m/s wurde von einem Lüfter mit Laminator und einer freien Öffnung von 220 mm Breite und 180 mm Höhe erzeugt. Mit diesem Aufbau wurden unter Verwendung entsprechender Waagen sowohl Auftriebs- als auch Widerstandsmessungen durchgeführt, die die bekannten Ergebnisse bestätigten und hier nicht dargestellt werden sollen.

Ergebnisse

Direkt an der Vorderkante des Flügels werden die folgenden Widerstandswerte gemessenen (R in kΩ): 1: 59; 2: 57; 3: 54; 4: 61; 5: 61. Der niedrigste Widerstandswert an der Spitze zeigt an, dass dort die Kühlung durch den Luftstrom am geringsten ist (Staupunkt). Stark dagegen ist die Luftströmung an den Rändern, wie  zu erwarten war.

In Abb. 3 ist die Widerstandsverteilung 50 mm hinter der Rückkante des Tragflügels dargestellt (x=250 mm). Die braune Kurve beschreibt die Strömungsverteilung ohne Tragfläche. Hinter der angestellten Tragfläche ist eine Fokussierung des Luftstromes in eine Richtung quer zur ursprünglichen Strömungsrichtung (Abwind) zu erkennen. Das Maximum des Widerstandswertes (gute Kühlung = große Luftdichte und/oder große Luftgeschwindigkeit) liegt nicht in Höhe der Hinterkante des Flügels, sondern weit darunter. Die Ablenkwinkel der Strömung von bis zu 45^o stehen mit dem Neigungswinkel der Tragfläche in keinem direkten Zusammenhang.

Abb. 3: Abwärtsbeschleunigung der Strömung durch den Flügel

Wie die Abbildung zeigt, steigt der Ablenkwinkel der Strömung (Abwind) zunächst mit zunehmenden Neigungswinkel der Tragfläche an, um bei höheren Neigungswinkel wieder abzunehmen.  Die Existenz eines Abwindes nicht nur bei einer Rotationsbewegung der Tragfläche (Hubschrauber), sondern auch bei einer linearen Translationsbewegung ist zwar nicht überraschend, unterstützt aber die Modellvorstellung der Entstehung des Auftriebes als Folge der Massenträgheit der Luft als kompressibles Medium, dessen Verhalten phänomenologisch bei isothermer Zustandsänderung durch die Zustandsgleichung idealer Gase beschrieben wird, die in der verkürzten Form lautet: p/ρ= const. Sinkt der Druck auf das Gas, so nimmt auch seine Dichte ab. Der Grund dafür liegt in dem Fehlen ausreichender Kohäsionskräfte (im Idealfall setzt man sie gleich Null).

Abbildung 4 zeigt die Widerstandswerte R(d) in verschiedenem Abstand x von der Vorderkante des Flügels bei einem Neigungswinkel von α= 10 ^o. 

Abb. 4: Messergebnisse zur Dichte/Geschwindigkeitsverteilung v*ρ in Abhängigkeit vom Abstand von der Tragflügeloberfläche in verschiedenen Abständen von der Vorderkante

Oberhalb des Flügels liegen die Widerstandswerte nahe am Flügel (kleine d) unter den mittleren Widerstandswerten, unterhalb dagegen darüber. Dieses Bild setzt sich über die ganze Flügeloberfläche bis zur Hinterkante fort. Erhöht man die Neigung der Tragfläche auf 23^o (Abb. 5), so ergibt sich im Vorderteil des Flügels eine ähnliche Verteilung der Widerstandswerte. Nur zur Hinterkante hin verändert sich das Bild: Es fehlt der Bereich mit deutlich geringeren Widerstandswerten in der Nähe der Oberfläche. Das als Coanda-Effekt bezeichnete Anschmiegen der Strömung an  den Fügel endet bei steigendem Anstellwinkeln dichter an der Vorderkante (Strömungsabriss). 

Abb. 5:  wie in Abb. 4, bei einem Anstellwinkel α= 23 ^o

Bemerkenswert ist die Abnahme (!) des Widerstandes (des Produktes aus Strömungsgeschwindigkeit und Dichte der Luft) im Bereich der beschleunigten Luft über dem Flügel. Die Annahme konstanter Luftdichte ist offenbar experimentell nicht haltbar. Die allgemein alleine zur Erklärung genutzte Geschwindigkeitszunahme der Strömung über der Tragfläche wird durch die Abnahme der Luftdichte sogar überkompensiert. Eine durch Reibung reduzierte Geschwindigkeit nahe am Flügel ist zwar denkbar, jedoch besitzt diese Region (Grenzschicht) nur eine Ausdehnung von weniger als einem Millimeter und ist damit für die Ergebnisse nicht relevant. 

Ergebnis: Modell der trägen Strömung

Zur Erklärung der Messungen ist damit - konform zur Beschreibung Lilienthals - ein Bereich reduzierter Dichte oberhalb der Tragfläche anzunehmen:

Der Raum über dem Flügel liegt bei angestelltem Flügel im "Windschatten" der Flügelspitze. Die Strömung der Luftmoleküle folgt den Gesetzen der Reibung und der Trägheit (Geradeausflug) und wird in Folge von Druckdifferenzen in und senkrecht zur Flugrichtung beschleunigt. Als Gegenkraft zur Abwärtsbeschleunigung des Luftstroms erfährt die Tragfläche selbst den Auftrieb. 

Offensichtlich ist, dass die abgelenkten Luftteilchen den Tragflügel nicht treffen dürfen, weil dadurch der Auftrieb verloren ginge. Damit wird die Form der gewölbten Tragfläche auch anschaulich verständlich: Sie ist optimiert in Hinblick auf die Erzeugung eines besonders stark ausgeprägten Coanda-Effekts.

Wenn man bei hohen Fluggeschwindigkeiten statt der isothermen Zustandsänderungen bei der Expansion der Luft im hinteren Teil des Tragflügels adiabatische in Betracht zieht, kann man mit diesem Modell auch die Vereisung von Tragflächen zwanglos erklären.

Die Autoren:
1) H. Kerkow †
2) B. Lukasch, Otto-Lilienthal-Museum Anklam